Histograms, Box & Whiskers Plots, and Other Made-Up-Sounding-Things: Continuing to Review and Asses Fundamentals

Histograms? That sounds hard...

Actually, everything we are going to talk about today is easy.

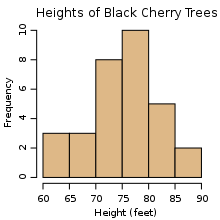
Histograms are a frequency table, that is, the height represents how frequently that value appeared. For example:

Apparently, the most common height for a Black Cherry tree in this study was between 75-80 ft.

Let's get some data about the class: maybe "when do you wake up?," "how tall are you?," and/or anything else interesting.

Now we'll chunk the data - divide it into bins. In the cherry tree example, the bins are "trees of height 60-65 feet, 65-70 feet,... etc" As a side note, when I say 60-65 and 65-70 are separate bins, what do I mean? Where does 65 go?

Alright, let's pick one of the measurements, put them in order from smallest to greatest, and find a few things:

The minimum (the smallest value)
The maximum (the largest value)
The median (median is the one in the middle)
The upper quartile (the number between the median and the maximum)
The lower quartile (the number between the minimum and the median)

If we were to graph those, we would get a Box and Whisker Plot:

Though they are always drawn horizontally in middle school math class, I have only seen them drawn vertically out in the wild:

Hopefully they still make sense when they are rotated.

Anyway, if you get that you should have no problem with your classwork. (Note: there are ideas in the classwork that I didn't explicitly say. But I gave you all the pieces you need to figure it out. And you can ask questions):

Shape of distributions

Clusters, Gaps, Peaks, and Outliers

Finally, for homework, continue working on these concepts (sorry for no links, use the search bar):

Comments

Marvin Minsky, AI, Math Education

The audio is too good to make this a gif. So, to be clear, this is the blog post for THURSDAY, 1/28. If you are looking for Tuesday's post, go back a post. I wanted to mention to you all that a mathematician and artificial intelligence researched named Marvin Minsky died on Sunday. Among lots of amazing things he did in his life, he wrote about math education for the OLPC (One Laptop Per Child) project. Here is that article ; I'd like you to read it for homework. Speaking of death, check out this amazing visualization ! Finally, for classwork, I would like you to go back to Tuesday's blog post, and comment on other people's homework. Specifically do you like the charts they chose? Are they interesting? Any feedback? Homework IMPORTANT: Pick which 5 (or more) variables that you will track for the Feltron project. Think about how you will keep track of them - pen and and notebook? The Reporter App? A pedometer? Also, that Marvin Minsky article is really

Statistical Studies - Tuesday 2/2/2016

Ok, today didn't go exactly as planned. If you saw the blog post I had up planned for today... we will get to that, but I incorrectly estimated how long some work would take you. Not your fault. You guys just move so fast through most material! You are working on the Statistical Studies topic on Khan Academy. It is not easy. That is okay. You don't have to get frustrated, or discouraged, or stressed. If it takes longer than I thought it would, I'll give you more time. Some good insights from the classwork: Go straight to the exercises, but go back to the videos if you are stuck If the videos feel too long, you can speed up playback (in the options menu, click the gear button). 1.25x isn't even noticeable. 1.5x is, but if you listen for a while you get used to it and can switch to 2x An "experiment" involves splitting a subset of the population you are looking at into two groups: one called the "control", who don't do anything diff

Monday 9/28

9/28/15 Monday Check in: Friday class & Homework Classwork: As long as we’re talking climate change... If someone tells you they don’t believe humans are causing it, you might want to ask them if smoking is bad for you. Why? There is as much evidence that humans are causing global warming as there is evidence that smoking causes cancer (you don’t have to click that link, I just like to put it up). Anyway, here’s a chart: It is entitled “Breakdown of the anthropic greenhouse gas emissions by gas, in billion tons carbon equivalent, in 2004” - it is a breakdown of the greenhouse gases emitted in 2004 that humans are responsible for. What’s the biggest greenhouse gas? What’s all that CO2 doing, and where does it go? A lot of it goes into the ocean, which seems better than the air, and it is... up to a point. The more CO2 in the ocean, the more acidic it gets (And the more acidic it gets, the lower its ph gets). That is fine... until it’s not. At some

Sam's Blog

Search This Blog